Sesión del 28/06/19
Examen Parcial 3

Sesiones del 26 y 27 de junio

Repaso de las proposiciones.

Sesión del 21/06/2019

Formas verbales de condicional

Implica, suficiente y necesaria

Formas de la condicional

Forma directa p -> q

Si llevo presentación entonces usaré cañonera

Forma recíproca q -> p

Usaré la coñonera si llevo la presentación

Forma inversa

~p -> ~q

Si no llevo presentación entonces no usaré cañonera

Forma contrapositiva

~q -> ~p

No usaré la cañonera si no llevo la presentación

Forma directa = forma contrapositiva

Forma recíproca = forma inversa 

Sesión del 25/06/2019

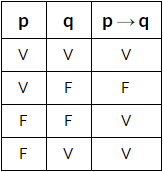
Proposición condicional

Una proposición condicional es aquella proposición que teniendo un antecedente deriva en una consecuencia, tiene una estructura “si p entonces q”.

Por ejemplo:

p: Saco 10 en mi próximo examen. q: Obtendré una beca.

Aplicando la estructura de una proposición condicional si p → q, donde p también es llamada antecedente o hipótesis y q consecuente, obtenemos:

Si saco 10 en mi próximo examen entonces obtendré una beca.

Tabla de verdad

Proposición bicondicional

Una proposición bicondicional también llamada de equivalencia ocurre cuando cuando la primera y la segunda proposición tienen el mismo valor lógico es decir cuando ambos son verdaderos o son falsos.

Su estructura p ↔ q se traduce a “p si y solo si q”, “entonces y solo entonces” o más comunmente a “q es equivalente a p”. No confundir equivalencia con igualdad.

Ejemplo:

a: Podré obtener mi licencia. (V) b: Apruebo el curso de conducción. (V)

a ↔ b: Podré obtener mi licencia si y solo si apruebo el curso de conducción.b ↔ a: Si apruebo el curso de conducción entonces y solo entonces podré obtener mi licencia.

Tabla de verdad

Sesión 19-6-19

Proposición compuesta 

En lógica matemática se dispone de los denominados operadores lógicos, que permiten modificar proposiciones, o asociar dos o más enunciados simples, convirtiéndolos en proposiciones compuestas.

Ejemplo: 

La raíz cuadrada de 25 es 5, o -5.

No todos los números primos son impares.

Mi cuñado es arquitecto e ingeniero.

Los aparatos tecnológicos son negros, blancos o grises.

Si tengo hambre pues cocino.

Proposición abierta

Son expresiones que contienen una variable y que al ser sustituidas dicha variable por un valor determinado, hace que la expresión se convierta en una proposición, pero sin alterar el orden. La proposición abierta es una expresión que tiene significado pero contiene por lo menos un término variable o indeterminado.

Ejemplos:

1. Tengo x dinero en el banco 

2. Alguien es un actor famoso 

Negación de las proposiciones 

Es una operación sobre un valor de verdad, típicamente, el valor de una proposición, que produce un valor de verdadero cuando su operando es falso, y un valor de falso cuando su operando es verdadero. Por tanto, si el enunciado A es verdadero, entonces ¬A (pronunciado "no A") sería consecuentemente falso; y lo contrario, si ¬A es verdadero, entonces A sería falso.

La tabla de verdad de ¬p es la siguiente:

Tabla de verdad de ¬p

p	¬p
Verdadero	Falso
Falso	Verdadero

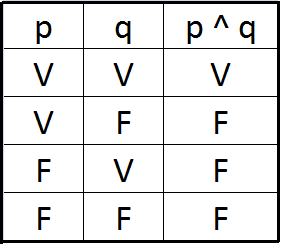
Conjución

Es cuando dos proposiciones simples se combinan mediante la expresión y  , la proposición compuesta resultante se le llama conjunción (pΛq). Su símbolo es: Λ, &, · 

Ejemplos:
La puerta está vieja y oxidada.Hace frío y está nevando.
Está lloviendo y es de noche.
Tiene gasolina y tiene corriente.

Simbolizacion

P ^ Q

F ^ V = F

Tabla de verdad

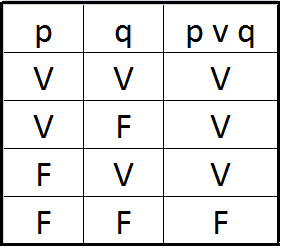
Disyunción 

 Se representan dos enunciados separadas por la expresión o basta con que una sea verdadera para que se cumpla la proposición  (pvq). Su símbolo es: V

Ejemplos:

Está lloviendo o es de noche.Está feliz o está enojado.Está caminando o está lloviendo.Hay derivadas o hay integrales.

Simbolización

P v Q

V v F = V

Tabla de verdad

Sesión 12/6/19

Ejercicios con Tangram

Sesión del 11/6/19

Ejercicios de construcción con ladrillos.

Sesión 7/6/2019
Resolver una ecuación de primer grado
La estrategia de utilizar una ecuación de primer grado para resolver un problema es muy importante, porque muchos problemas de las ciencias, la economía, las finanzas, la medicina y de otro campos se pueden plantear en términos de una ecuación.

Sesión del 6/06/2019
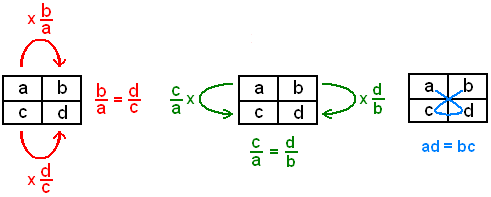
Estrategia proporcionalidad o porcentajes

Razón: Es el resultado de comparar dos cantidades y siempre es un número real. En la razón x : y (se lee x es a y), donde a x se le llama antecedente, y a y consecuente. 

Proporción: Se le llama proporción a la igualdad de dos razones. Una proporción se puede escribir como a : b : : c : d (se lee a es a b como c es a d). 

Porcentaje: Es una razón en la cual el consecuente es 100. 

Ejemplo:n

Sesión del 13/6/19
Gráficas estadísticas
 Es un tipo de representación de datos, generalmente numéricos, mediante recursos visuales (líneas, vectores, superficies o símbolos), para que se manifieste visualmente la relación matemática o correlación estadística que guardan entre sí.


Gráficas de barras
También conocido como gráfico de barras o diagrama de columnas, es una forma de representar gráficamente un conjunto de datos o valores, y está conformado por barras rectangulares de longitudes proporcionales a los valores representados.



Gráfica de líneas
muestran una serie como un conjunto de puntos conectados mediante una sola línea.




Pictograma
Dibujo o signo gráfico que expresa un concepto relacionado materialmente con el objeto al que se refiere.


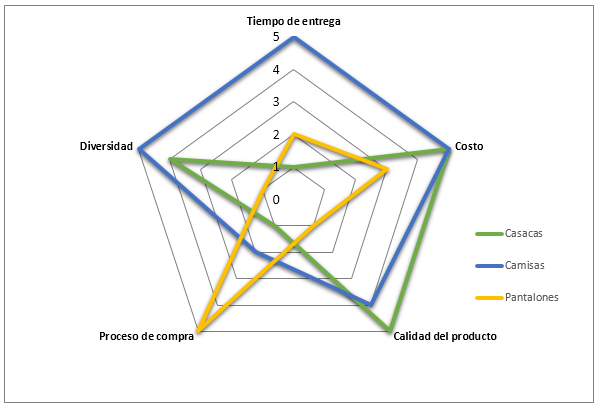
Gráfica radial

Gráfico de Araña, Gráfico de Red, Gráfico Polar y Gráfico de Estrella. Los gráficos radiales son una forma de comparar múltiples variables cuantitativas. Esto los hace útiles para ver qué variables tienen valores similares o si hay valores atípicos entre cada variable.

4/6/19
Primer examen parcial

Sesión 8 31/05/2018
Estrategia de trabajar hacia atrás

La estrategia de trabajar hacia atrás consiste en que, a partir del dato final o la solución, ir pensando hacia atrás, paso a paso, hasta llegar a los datos originales. se precede a recorrer la secuencia de pasos al contrario para ir de los datos conocidos a la solución.

Sesión 7 30/05/2019
La estrategia de hacer un diagrama es útil para identificar en ellos datos e incógnitas del problema.
En la figura se colocan todos los datos conocidos que da el problema y los datos que se pretende encontrar, esto nos ayuda a tener una mejor idea y visualización de lo que el problema pide.

Sesión 6 29-05-2019
Utilización de un cuadro o lista

La estrategia de cuadro o lista es útil al resolver los problemas, pues colocando lo datos en una lista se identifican mejor las incógnitas del problema.

SESIÓN 7-6-2019

Ecuaciones de Primer Grado
Ecuación: igualdad de dos expresiones que incluyen términos conocidos, variables e incognitas.

Problema:
La suma de las edades de tres personas es 112 años. La mayor tiene 20 más que la menor, la del medio tiene 18 años menos que la mayor. hallar las respectivas edades.

Pasos de Polya:
Paso 1:
Las edades de tres personas suman 112 años, debo encontrar la edad de cada una.

Paso 2 Trabajar con ecuaciones o con cada variable.

Paso 3.

Mayor + Medio + Menor = 112

x=menor
x+20= mayor
x+20-18= medio

x+20+ (x+20-18)+x=112
x+20+x+2+x)112
3x+22=112

3x=112-22
3x=90
x=90/3
x=30
Menor= 30
Mayor= 30+20= 50
Medio= 30+20+18=32

Paso 4 Prueba
30+50+32=112

30+20+(30+20-18)+30=112
50+32+30=112
112=112

Sesión 5 28-05-2019

1. Repaso de los pasos de POLYA

Paso 1:
Identificar el problema
Entender el problema
Formular la pregunta

Paso 2
La forma en la que se va a resolver el problema,

Paso 3
Resolver el problema

Paso 4
Realizar la prueba

2. Buscar un patrón

2  4  6  8, el patrón es 2 por lo que el siguiente número es 10
1  4  9  16, el patrón es el numero siguiente al cuadrado, es decir que el siguiente número es 25.


Problema: