Sesión del 5/7/19

Relación conectivos lógicos y operaciones de conjuntos

Conectivos lógicos

Conjunción

Sesión del 2/7/19

Conjuntos:

Un conjunto se define como la agrupación de diferentes elementos que comparten entre sí características y propiedades semejantes. Estos elementos pueden ser cualquier cosa, tales como números, canciones, meses, personas, etcétera.

A su vez un conjunto puede convertirse también en un elemento. Por ejemplo, un ramo de flores. En principio una flor sería el primer elemento, pero al conjunto de flores se lo puede considerar luego como un ramo de flores, convirtiéndose así, en un nuevo elemento.

Formas de describir los conjuntos

Diagrama de Venn

El diagrama de Venn no es más que la representación gráfica de los conjuntos. Es decir, cuando los elementos que componen el conjunto se encuentran dentro de una superficie limitada por una línea:

Imagina que tienes una bolsa en la que  hay diferentes frutas. Entonces, al traducirlo como un conjunto  se vería la  como lo que representa todas frutas. El círculo sería la bolsa y lo que se encuentra adentro, en este caso cada una de las frutas (manzana, banano, naranja) serían los elementos que forman el conjunto de las frutas.

Conjunto universo:

es un conjunto formado por todos los objetos de estudio en un contexto dado.

Operaciones de conjuntos:

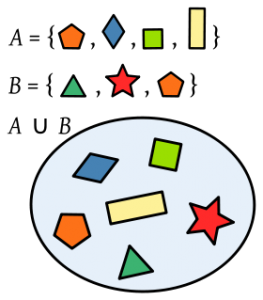
1. Unión de conjuntos

La operación se denomina unión de conjuntos, y da como resultado un nuevo conjunto formado por todos los elementos que pertenecen a ambos conjuntos. Escrito con símbolos, la unión de dos conjuntos (por ejemplo llamados G y H) se denota así:

 G  ∪  H

Si queremos expresarlo en diagramas de Venn, deben primero representarse   todos los elementos en sus respectivos conjuntos y luego incluyen todos (sin repetirlos) en un mismo diagrama. En la siguiente imagen, se puede apreciar esta definición con mucha claridad. Presta atención:

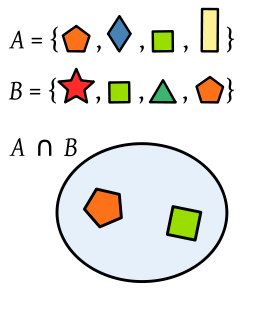
2. Intersección 

Realizar la intersección de dos o más conjuntos, es definir un nuevo conjunto formado solamente por aquellos elementos que estén presentes en todos los conjuntos en cuestión. En otras palabras: sólo forman parte del nuevo conjunto, los elementos que tengan en común.

Existe un símbolo matemático para la intersección. Para poner un ejemplo,la intersección de dos conjuntos llamados G y H se denota de la siguiente manera:

G  ∩ H

En vez de ejemplificar en diagramas, esta vez veremos cómo se representa la interescción de conjuntos definida por extensión.

Primero definimos a los respectivos conjuntos:

G = { a, b, c, d, e, f, g, h }

H = { a,e,i,o,u }

G  ∩ H = { a,e }

En efecto, a y e, son los únicos elementos en común, es decir que están presentes en los dos conjuntos a la vez.

3.Diferencia de conjuntos:

La diferencia de dos conjuntos A y B, que se escribe A - B, se define como el conjunto formado por los elementos A que no pertenecen a B.

La diferencia de conjuntos las podemos representar en diagramas de Venn de la siguiente forma;

a) Cuando los dos conjuntos tienen elementos en común la diferencia se representa de la siguiente forma;

b) Cuando los conjuntos no tienen elementos en común, la diferencia es igual al conjunto A y se representa;

c) Cuando todos los elementos de A pertenecen a B la diferencia es igual a conjunto Vacío (ᴓ), y se representa;

d) Cuando todos los elementos del conjunto B pertenecen a A, la diferencia se representa;

Ejemplo:

Sean los conjuntos A = { 2, 4, 6, 8, 10 } y B = { 1, 2, 3, 4, 5} .

¿Cuál es la diferencia de A - B?

4. Diferencia Simétrica:

La diferencia simétrica de dos conjuntos A y B, que se escribe A Δ B, se define como la diferencia de A U B y A ∩ B.

La diferencia simétrica de conjuntos las podemos representar en un diagrama de Venn de la siguiente forma;

a) Cuando los dos conjuntos tienen elementos en común la diferencia simétrica se representa de la siguiente forma;

b) Cuando los conjuntos no tienen elementos en común, la diferencia simétrica es igual al conjunto A U B y se representa;

c) Cuando todos los elementos de A pertenecen a B, la diferencia simétrica es igual B - A, y se representa;

Ejemplo:

Sean dos conjuntos A = { a, b, c } y { a, b, c, d, e, f } ¿Cuál es la diferencia simétrica de A y B? 

5. Complemento de un conjunto:

Dado el conjunto A ϵ U, se define el conjunto complementario de A, que se escribe A^c, el cual está formado por los elementos que pertenecen al conjunto universal (U), pero que no pertenecen a A.

El conjunto complemento de A lo podemos representar en un diagrama de Venn de la siguiente forma;

Es decir, también podemos interpretarlo como;

Ejemplo:

Sea U = { a, e, i, o, u } y A = { i, u } ¿cuál es el complemento de A?

Entonces, si quitamos las letras i y u, obtenemos A^c.

6. Producto cartesiano 

El producto cartesiano de dos conjuntos es una operación, que resulta en otro conjunto, cuyos elementos son todos los pares ordenados que pueden formarse de forma que el primer elemento del par ordenado pertenezca al primer conjunto y el segundo elemento pertenezca al segundo conjunto.

 Si el conjunto A está formado por los elementos 3, 5, 7 y 9, mientras que el conjunto B alberga los elementos m y r, el producto cartesiano de ambos conjuntos es el siguiente:

A x B = {(3,m), (3,r), (5, m), (5,r), (7,m), (7,r), (9,r), (9,r)}

El producto cartesiano, por lo tanto, está formado por todos los pares ordenados que se pueden formar a partir de dos ciertos conjuntos. Cada par ordenado se constituye por dos elementos: el primer elemento pertenece a un conjunto y el segundo elemento, al otro. Si seguimos con nuestro ejemplo, en el par ordenado (3,m), 3 es el primer elemento (corresponde al conjunto A) y m es el segundo elemento (perteneciente al conjunto B).

Es importante establecer, además de todo lo expuesto, que cuando hablamos de productos cartesianos tenemos que hacer referencia a dos casos o tipos de generalizaciones posibles. Así, por un lado, se encuentra el llamado caso finito, que es aquel que parte de un número finito de conjuntos (A1, A2, A3…An). Del mismo su producto cartesiano vendría a ser el grupo de listas numeradas cuyo elemento está en A1, el segundo en A2…

El caso infinito sería aquel en el que, partiendo de una gran familia de conjuntos con toda la probabilidad infinita y de carácter arbitrario, a la hora de definir el pertinente producto cartesiano se sustituiría lo que es la definición de las mencionadas listas numeradas por otra.

Sesión del 28/06/19
Examen Parcial 3

Sesiones del 26 y 27 de junio

Repaso de las proposiciones.

Sesión del 21/06/2019

Formas verbales de condicional

Implica, suficiente y necesaria

Formas de la condicional

Forma directa p -> q

Si llevo presentación entonces usaré cañonera

Forma recíproca q -> p

Usaré la coñonera si llevo la presentación

Forma inversa

~p -> ~q

Si no llevo presentación entonces no usaré cañonera

Forma contrapositiva

~q -> ~p

No usaré la cañonera si no llevo la presentación

Forma directa = forma contrapositiva

Forma recíproca = forma inversa 

Sesión del 25/06/2019

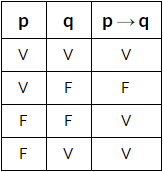
Proposición condicional

Una proposición condicional es aquella proposición que teniendo un antecedente deriva en una consecuencia, tiene una estructura “si p entonces q”.

Por ejemplo:

p: Saco 10 en mi próximo examen. q: Obtendré una beca.

Aplicando la estructura de una proposición condicional si p → q, donde p también es llamada antecedente o hipótesis y q consecuente, obtenemos:

Si saco 10 en mi próximo examen entonces obtendré una beca.

Tabla de verdad

Proposición bicondicional

Una proposición bicondicional también llamada de equivalencia ocurre cuando cuando la primera y la segunda proposición tienen el mismo valor lógico es decir cuando ambos son verdaderos o son falsos.

Su estructura p ↔ q se traduce a “p si y solo si q”, “entonces y solo entonces” o más comunmente a “q es equivalente a p”. No confundir equivalencia con igualdad.

Ejemplo:

a: Podré obtener mi licencia. (V) b: Apruebo el curso de conducción. (V)

a ↔ b: Podré obtener mi licencia si y solo si apruebo el curso de conducción.b ↔ a: Si apruebo el curso de conducción entonces y solo entonces podré obtener mi licencia.

Tabla de verdad

Sesión 19-6-19

Proposición compuesta 

En lógica matemática se dispone de los denominados operadores lógicos, que permiten modificar proposiciones, o asociar dos o más enunciados simples, convirtiéndolos en proposiciones compuestas.

Ejemplo: 

La raíz cuadrada de 25 es 5, o -5.

No todos los números primos son impares.

Mi cuñado es arquitecto e ingeniero.

Los aparatos tecnológicos son negros, blancos o grises.

Si tengo hambre pues cocino.

Proposición abierta

Son expresiones que contienen una variable y que al ser sustituidas dicha variable por un valor determinado, hace que la expresión se convierta en una proposición, pero sin alterar el orden. La proposición abierta es una expresión que tiene significado pero contiene por lo menos un término variable o indeterminado.

Ejemplos:

1. Tengo x dinero en el banco 

2. Alguien es un actor famoso 

Negación de las proposiciones 

Es una operación sobre un valor de verdad, típicamente, el valor de una proposición, que produce un valor de verdadero cuando su operando es falso, y un valor de falso cuando su operando es verdadero. Por tanto, si el enunciado A es verdadero, entonces ¬A (pronunciado "no A") sería consecuentemente falso; y lo contrario, si ¬A es verdadero, entonces A sería falso.

La tabla de verdad de ¬p es la siguiente:

Tabla de verdad de ¬p

p	¬p
Verdadero	Falso
Falso	Verdadero

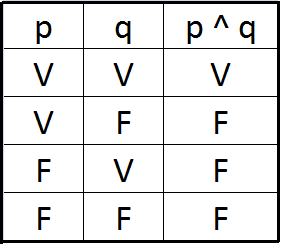
Conjución

Es cuando dos proposiciones simples se combinan mediante la expresión y  , la proposición compuesta resultante se le llama conjunción (pΛq). Su símbolo es: Λ, &, · 

Ejemplos:
La puerta está vieja y oxidada.Hace frío y está nevando.
Está lloviendo y es de noche.
Tiene gasolina y tiene corriente.

Simbolizacion

P ^ Q

F ^ V = F

Tabla de verdad

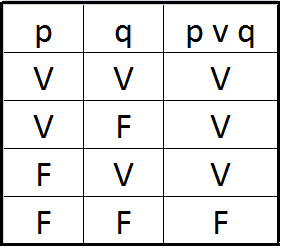
Disyunción 

 Se representan dos enunciados separadas por la expresión o basta con que una sea verdadera para que se cumpla la proposición  (pvq). Su símbolo es: V

Ejemplos:

Está lloviendo o es de noche.Está feliz o está enojado.Está caminando o está lloviendo.Hay derivadas o hay integrales.

Simbolización

P v Q

V v F = V

Tabla de verdad